No.79　受注間隔とリードタイムが変動すると、受注件数の分布形状は？

納入リードタイムがバラツクとき、受注件数のバラツキにどのような影響をおよぼすか、数式と分布形状で確認してみました。これまでは、分布形状は離散型待ち行列理論ベースのシミュレーションで分析しておりましたが、今回は、身近にあるエクセルを使って計算しました。結果はシミュレーションとほぼ同じ。シミュレーションよりエクセルの方がずーっと簡単です。エクセル、使えそうです。

前回は納入リードタイムの影響をみるために、受注間隔は一定という条件で計算してみましたが、今度は、受注間隔がランダムに変動する場合、受注件数の分布形状はどうなるか、エクセルで計算してみたいと思います。

店に来る客数、ATMで並ぶ列の長さや待ち時間、スーパーマーケットのレジの待ち行列、電話のトラフィック、インターネットのアクセス、、などなど。これらの事象は待ち行列理論で詳しく説明されています。受注間隔がランダムに変動する受注件数に関しても同じように待ち行列理論を適用することができます。待ち行列理論ではランダムに到着する注文の時間間隔の分布として、指数分布がよく使われます。指数分布で到着する注文件数をある時間間隔でカウントすると、その件数はポアッソン分布することが知られています。指数分布、ポアッソン分布、待ち行列理論については専門書等をご参照頂くとして、ここでは、受注件数の分布をポアッソン分布として、話を進めてみたいと思います。

レビューしてみます。
① 納入リードタイム（LT）変動；固定LT＋ガンマ分布
② 納入LT変動による受注件数の変動；（固定LT＋ガンマ分布）/注文の到着間隔
③ 注文の到着間隔；指数分布
④ 納入LTでの受注件数；ポアッソン分布
⑤ 注文の到着間隔と納入LTが変動するときの受注件数のバラツキ分布

①と②については前回説明しました。今回は注文の到着間隔がランダムに変動し、納入リードタイムが変動する場合、受注件数のバラツキがどうなるかを調べます。納入リードタイムが一定のとき、指数分布で到着する注文件数はポアッソン分布しますが、それが変動するとどうなるか。つまり、④の分布に②の変動を加えたときの分布はどうなるか、を調べてみます。

エクセルでの計算方法について、図１で説明します。納入リードタイムの分布はF列とG列、納入リードタイム変動による受注件数の分布はL列とM列に示してあります。受注間隔の平均は10（セル；J5）の指数分布、受注件数の分布はポアッソン分布となり、O列の件数ごとの発生確率がそれぞれP列に示されています。この確率は納入リードタイムが変動しないときの確率ですが、納入リードタイムが変動するとL列とM列で示される分布に従うことになります。

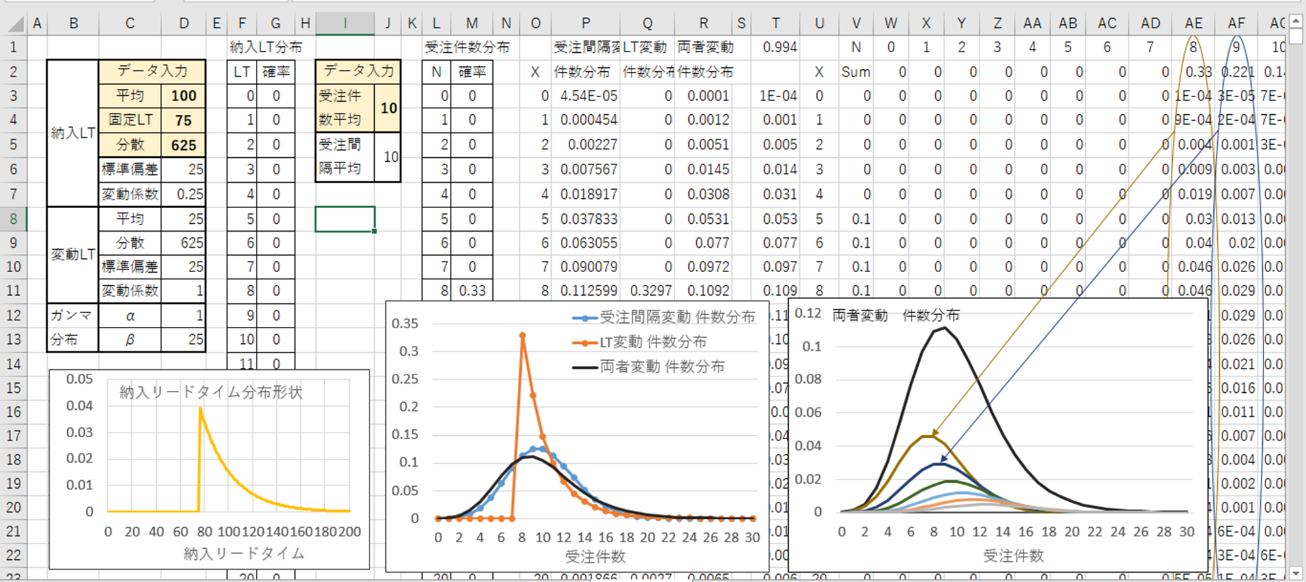
図1 受注間隔がランダム、納入リードタイムが変動するときの受注件数の分布形状

受注間隔が指数分布に従うとき、ポアッソン分布に従う受注件数は、納入リードタイムの変動により、どのようになるかを考えてみます。例えば納入リードタイムが長くなるとその間の受注件数は増えます。納入リードタイムは連続値ですが、計算は受注件数の増加を1件ごとに計算することにします。

セル；W1、X1、Y1、、は0、１、２、、、という数字が入っていますが、これは受注件数の平均値を示します。一方、セル；U3、U4、U5、、は横軸の受注件数を示します。例えばセル；AE5をみてみますと、
POISSON.DIST(U5,$AE$1,FALSE)*$M$11
となっています。これは、平均8（セル；AE1）のポアッソン分布の2件（セル；U5）の確率に受注件数８の発生確率（セル；M11）をかけてセル；AE5の確率を計算しています。セルAE6は、
POISSON.DIST(U6,$AE$1,FALSE)*$M$11
で、ポアッソン分布の3件（セル；U6）の確率を計算しています。このようにして、AE列は納入リードタイムが変動した場合、平均８のときの受注件数０、１、２、、、の発生確率となります。分布形状はグラフで示すように平均８の山形の分布となります。同様に平均９の件数分布はAF列、平均10の件数分布はAG列、、、となります。

列ごとの分布が重ね合わされて件数ごとの発生確率となりますので、件数ごとに行方向に合計した値をR列に示しています。

図2は納入リードタイムの変動係数は0.25のままで、固定部分を65としたときの計算例です。

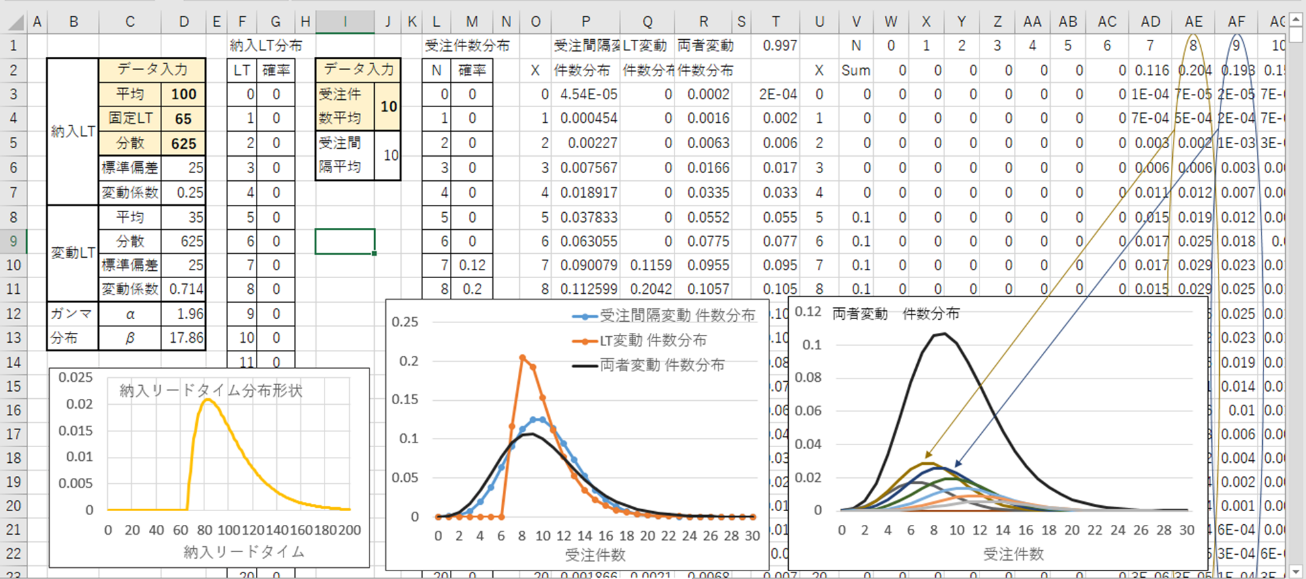
図2　納入リードタイムの変動係数0.25で固定リードタイムを65とした場合

図3は納入リードタイムの変動係数は0.25のままで、固定部分を0としたときの計算例です。

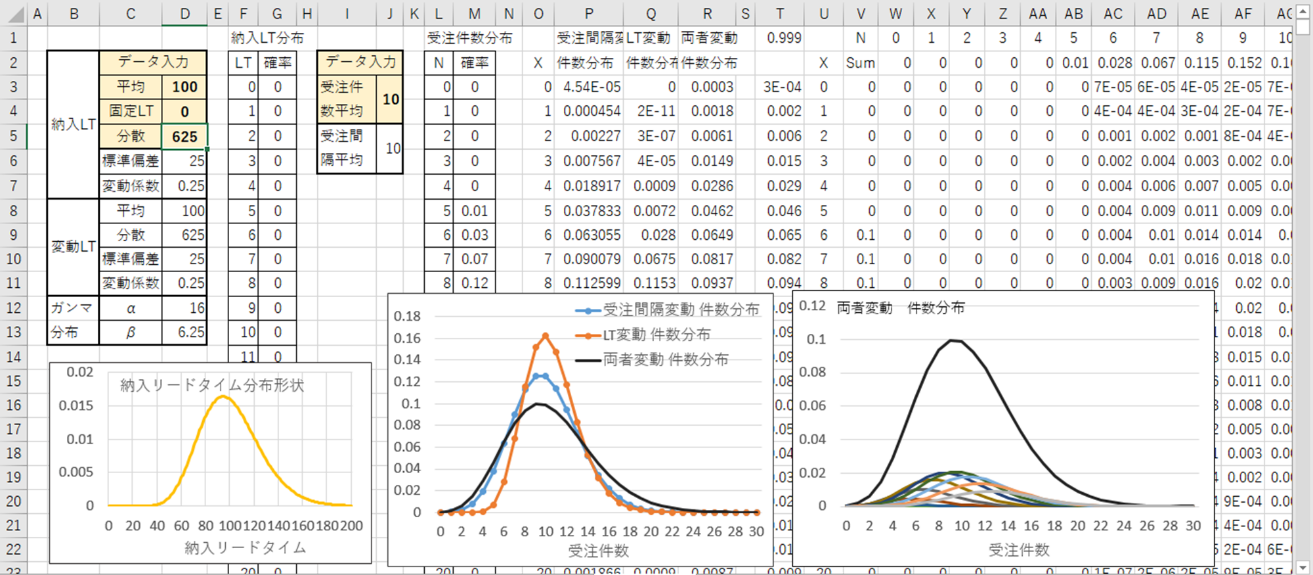
図3　納入リードタイムの変動係数0.25で固定リードタイムを0とした場合

図4は納入リードタイムの変動係数を0.5、固定部分を50としたときの計算例です。

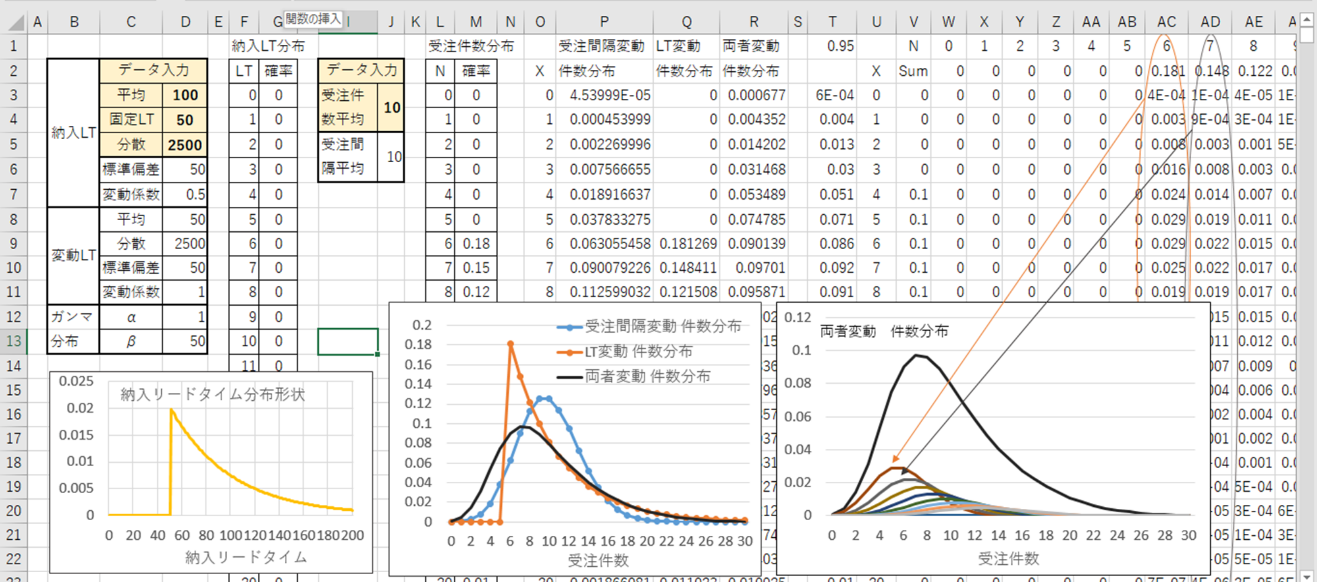
図4　納入リードタイムの変動係数を0.5にした時の受注件数の分布形状

エクセルで分布形状を計算することができました。しかしこの計算結果は実用的に使えるのかどうか、多少心配になります。待ち行列理論をベースにした離散型のシミュレーションソフトで確認してみましょう。シミュレーションでは乱数を使いますが、使う乱数によって結果が多少異なります。3種類の乱数を使ってシミュレーションを行ってみました。結果の一例を図5に示します。シミュレーション結果とエクセルでの計算結果はよくあっています。

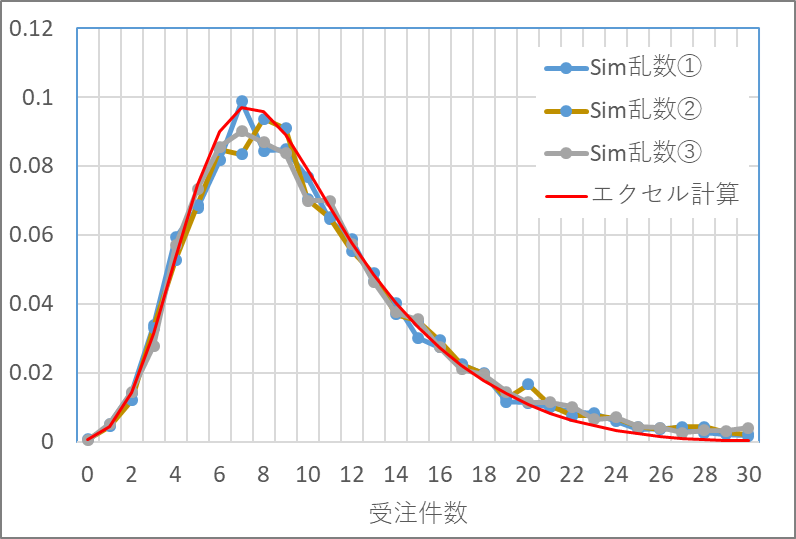
図5　待ち行列理論離散型シミュレーションとエクセル計算の比較

受注間隔と納入リードタイムが変動する場合の受注件数の分布をエクセルで計算してみました。受注1件で注文数が必ず1個であれば、注文件数＝注文数　となりますが、実際は1回の注文での注文数はさまざまです。1件当りの注文数；Qを考慮すると、需要分布はどうなるのでしょうか。次回、検討してみたいと思います。