No.88　ポアッソン分布が暴く“出荷確率”の虚

前回（No.87）で安全在庫の計算に出荷確率（出荷率）を使うという提案を見つけ、考えてみました。この説、https://www.sakata.co.jp/logistics-401/　で引用されているだけではなく、その他でも使われております。2例ほど、示しておきます。

[出典１]　「適正在庫の考え方・求め方」　日刊工業新聞社　勝呂隆男著　p.115～p.116

間欠需要の場合の安全在庫算出式は次のようになる（季刊輸送展望2002春号p.79を参考に作成）。

・定期発注方式の場合

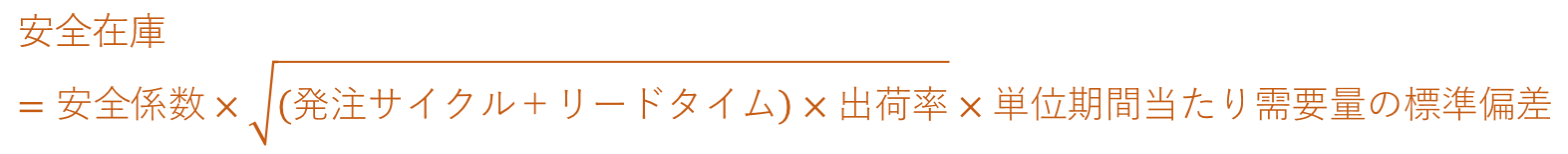
・発注点方式の場合

出荷率は、次のように計算する。

標準偏差の計算は、出荷がゼロであった日のデータをカウントしないで算出する必要がある。

[出典２]　「在庫管理の基本としくみがよ～くわかる本」　秀和システム　湯浅和夫他著p.76~.78

出荷がない日は「平均出荷量」の計算対象から除く――（説明等省略）――

出典２について補足しておきます。ある期間の平均出荷量を計算するとき、ある期間を（出荷のあった日数＋出荷のなかった日数）としますと、平均出荷量の計算は出荷日数のみを使い次のように計算する、ということになります。

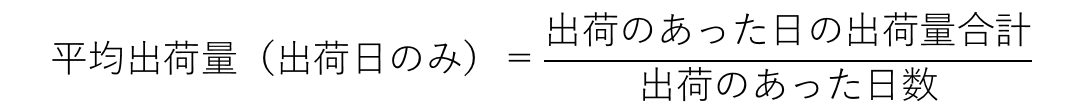
一般的平均出荷量は次の式で計算します。

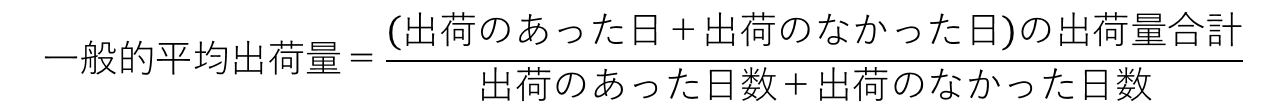
出荷のなかった日の出荷量合計は０ですので、

出荷のあった日の出荷合計＝一般的平均出荷量×（出荷のあった日数＋出荷のなかったに日数）

となり、平均出荷量（出荷日のみ）を一般的平均出荷量で表すと次のようになります。

出荷確率という言葉は使っておりませんが、“出荷のない日を除く”とは、出荷確率を使って計算していることになります。

出荷確率で分散などを補正するこの種の考え方が出てきたのは2000年初め。今日（2019年6月）まで、約20年弱、特に異論もなく、受け入れられてきたようです。両書籍とも、比較的初心者向けであることも、異論が出ない背景となっていたのかもしれません。逆にみれば、出荷確率という考え方が「正しい」と受け止められてきたのではないか、とも思います。

この出荷確率の考え方の正誤を判断するためには、在庫管理の最も基本的且つ理論的な在庫補充の原理に言及しなければなりません。在庫管理の基本機能は、需要（受注量、出荷量、、）にいかに追従し在庫補充を行うか、ですが、このとき重要となるのは需要をいかに迅速、且つ正確に捉えるかです。

多少小難しい話になって恐縮ですが、論理性を重視して確率分布で説明することにします。需要は注文が来て実現します。注文はある時間間隔で来ます。その時間間隔はランダムだとすると、その分布は指数分布することが知られています。需要を時間間隔で捉えるのは判りづらいので、ある期間（1日とか、1週間とか、、）に来る受注件数で表すのが普通です。1日に5件だとか10件だとか、ということになります。この受注件数の分布がどうなるかですが、ポアッソン分布という分布に従うことがわかっております。

もうひとつ考えておく必要があることは、1件の受注で10個のときもあれば50個のときもあることです。受注1件当りの受注数量もばらつき、それが加わってある期間の受注数量となるわけです。

ここで重要なことは、ある期間の需要（受注量、出荷量、、）は受注件数と1件当りの受注数量の2つの要素で決まるということです。

この2つの要素を含めますとわかりにくくなりますので、ここでは、1件当りの受注数量を１個として、受注件数＝受注数量という条件で考えてみます。こうすれば受注件数だけについて考えればいいことになります。

そうしますと、受注間隔の分布である指数分布とある期間の到着受注件数の分布であるポアッソン分布でそれらの性質を調べればいいことになります。

ランダムに来る（指数分布に従う）注文の入り具合を具体的な数値を使ってみてみましょう。図１をご覧ください。平均到着間隔は４（日）とします。6日目に1個、9日目に1個、、、25日目には2個の注文が来ました。53日目には3個の注文が入りました。注文があったのは90日中15日だけ、残りの75日の注文は０です。

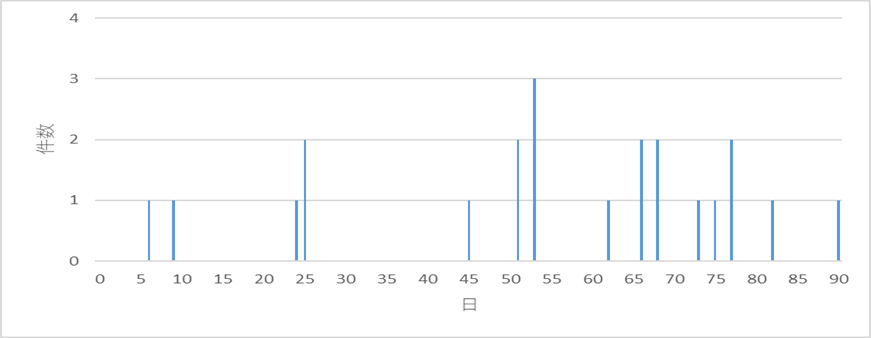
図１　指数分布する平均到着間隔4（日）の注文の到着の一例

時間間隔の分布形状は図２に示すような指数分布です。

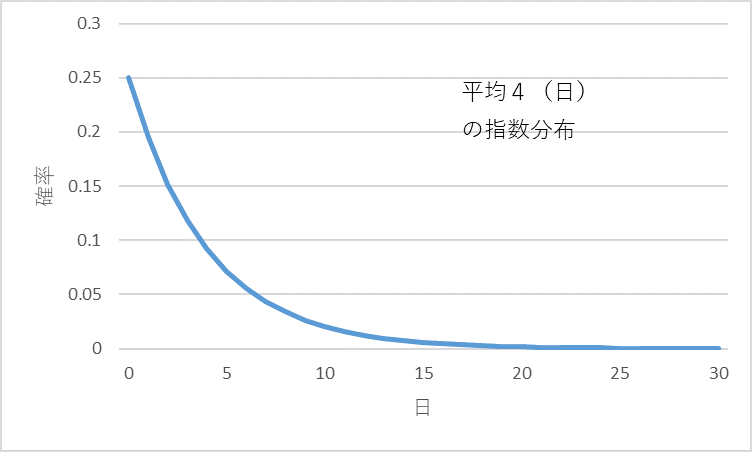
図2　平均４（日）の指数分布

これを受注数で集計してみます。このとき、集計間隔を決める必要があります。集計間隔を4（日）とすれば、注文の到着間隔が４（日）ですので、受注数は平均１のポアッソン分布に従います。集計間隔を８（日）にすれば平均２のポアッソン分布、集計間隔を16（日）にすれば平均４のポアッソン分布となります。一例を図３に示します。

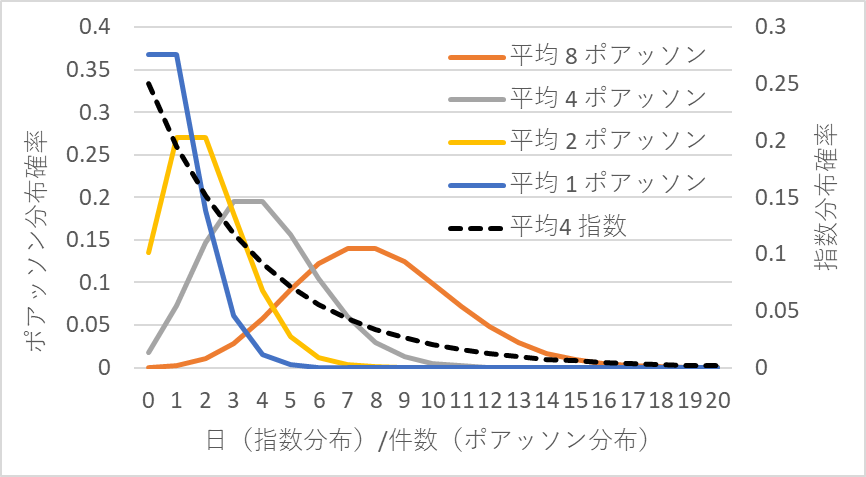
図３　平均4（日）の指数分布に対するポアッソン分布の例

集計間隔を２（日）とすれば平均0.5、集計間隔を1（日）とすれば平均0.25、集計間隔を0.5（日）とすれば平均0.125のポアッソン分布となります。図４に例示します。

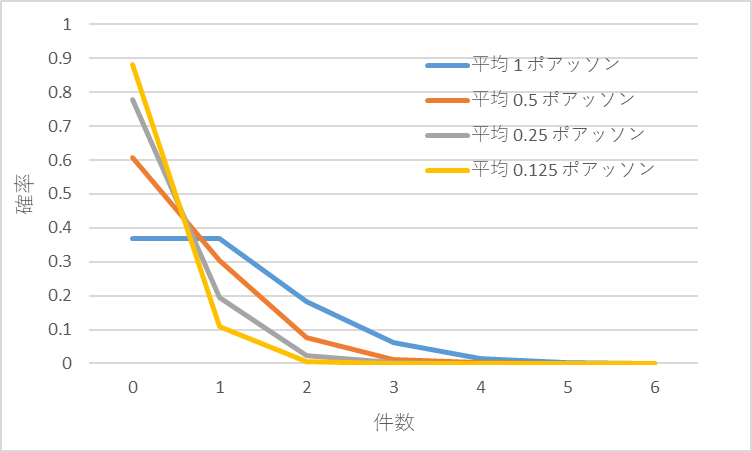
図４　平均１以下のポアッソン分布の分布形状

ポアッソン分布は平均が大きくなると正規分布に似てきます。だいたい平均５～６以上では正規分布として扱うことができると言われております。しかし、平均が小さくなると、ゼロの確率が高くなり、特に平均が1以下では正規分布とはかけ離れた形状になります。

では、ポアッソン分布の分散や標準偏差はどのようになるのでしょうか。実は、ポアッソン分布には面白い性質があります。ポアッソン分布の分散はその分布の平均値と同じ値になります。平均がわかれば分散は計算しなくてもすぐにわかります。

事例は、90日中75日は注文のない典型的な間欠需要パターンです。出荷確率は17％となりますが、受注数量の平均や分散を求めるとき、出荷確率なんてどこにも出てきませんね。受注数量の分布は、ここでは簡単にするため1件当りの出荷数（受注数）を１としていますので、ポアッソン分布に従います。ポアッソン分布の平均も分散も出荷確率とは、まったく関係ありません。

間欠需要の受注量（出荷量）の平均や分散を算出するとき、出荷確率を用いることは、間違いである、ということをなんとなく、お判りいただけたと思います。