No.82 限られたデータで推定する間欠需要分布

前回は、受注件数はポアッソン分布、量/件はガンマ分布すると仮定して、間欠需要での需要分布形状などを調べてみました。

しかし、現実をみれば、間欠需要ではデータ数が少ない。データ数が少ないと分布を特定することは難しくなります。ポアッソン分布だ、ガンマ分布だなんて、わからないわけです。データ数を増やすとなると、さらに1～2年かかっちゃう。その間、無管理状態でいい分けないですよね。

で、今回のテーマは、受注件数の分布も、量/件の分布もわからないとき、適正在庫をどのようにして求めるのか。分布が特定できませんので、分布のパラメータを使うことはできません。パラメータを使えないとなれば、、どうしましょうか。困りましたね。コペルニクス的発想の転換が必要なんでしょうかね。そんな大それたことは後にして、実際のデータをみてみましょうか。表１に例示するデータで考えてゆくことにします。

表１は月ごとの受注数量を示しています。1月は3件の注文があり、それぞれ13個、13個、7個で計33個。2月から5月まで注文はなし。6月は1件の注文があって12個、、という具合です。受注1件の受注数量を量/件と表記することにします。

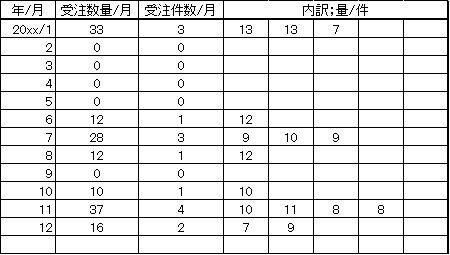
表1　ある商品の1年間の月ごとの受注数量

受注数量/月の度数分布を描いてみると図１のようになります。注文がゼロの月が5回、10個の注文があった月は1回、12個が2回、16個が1回、、。

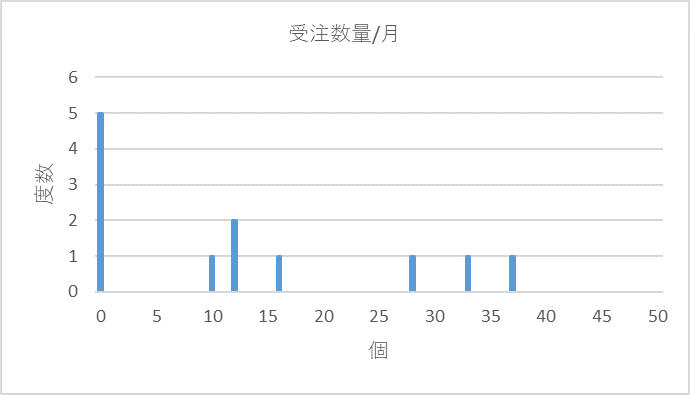
図１　受注数量/月の度数分布

通常の需要では、これが正規分布に近似するんですが、図１の分布はどう見ても正規分布ではありませんね。形だけではなく、歯抜け状態ですから、サービスレベルに対する適正在庫の設定もうまく出来そうもありません。

今の需要を把握するやり方は、表１の左の2列を使って、3列目より右側にあるデータは使いません。でも、これらのデータは、商取引があれば、必ず残る情報です。手間暇かけてとらなければならないたぐいのデータではありません。2列目の受注数量の内訳詳細情報が3列目より右側です。情報が限られているとなれば、このデータで補うことはできないものか。

3列目の受注件数/月と量/件のデータの度数分布をグラフにしますと図２、図３のようになります。

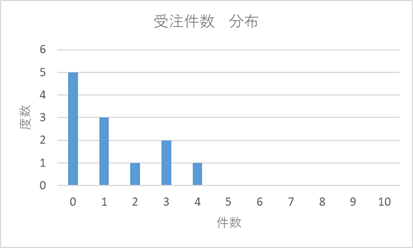
図２　受注件数の分布　

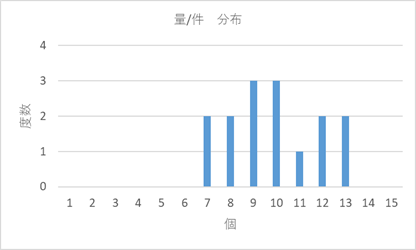
図３　量/件の分布

これを、うまく利用できないか、ということなんですが。それぞれの分布、特徴をみてみましょう。量/件の分布は正規分布っぽいところがありますが受注件数の分布は正規分布とは似てませんね。ポアッソン分布とかガンマ分布とかにはどうですかね、、。うーん、似てるかなぁ～、やっぱ、似てませんね。

ちょっと、ちょっと、、近似できる分布はどんな分布か、というアプローチでしたっけ。分布形状に関する情報はないことにしたんですから、そのようなやましい気持ちは捨てましょう。

でも、ちょっと未練はありますね。どんな？　受注件数の分布と量/件の分布から月間の受注数量の分布を計算できるんですよねぇ～。そうそう、できるんですよ。次の式で。

受注件数の平均；、その分散；Vn、量/件の平均；、その分散；Vqとして、月間受注量平均；、その分散；Vdとすると、

この式、一般の需要環境はもちろん、間欠需要でも成り立つんです。分布形状に関係なく成り立つ。但し、データ数が少ないと、ズレが大きくなりますけどね。また、離散型のデータなので、ドンピシャリと一致するわけではありませんが、、。

でも、分布形状が異なると累積確率カーブも違ってきますから、どんな確率分布かわかんないとサービスレベルに対する安全在庫を正確に計算することはできない。残念でした、、。

未練は捨てて、分布形状がわからないことを意識して、考えてみましょう。分布のパラメータは使えませんので、それに代わる手がかりを探してみましょう。

表１をじっと見てみます。どのようなメカニズムで需要が発生しているかを、、。月間受注数量は月に何件の注文があるか（受注件数/月）、注文ごとの数量（量/件）はいくつか、で決まります。いたって単純なメカニズムですね。受注件数もランダム、量/件もランダムとしましょう。

で、表１が実際のデータです。背後に受注件数の母集団と量/件の母集団があって、それから抜き取られたのが表１のデータだ、と考えます。受注件数と量/件は互いに独立で、それぞれの母集団は変わらないと仮定します。

表１の1年間のデータから、例えば次の1年間の受注件数、量/件を推定してみます。受注件数はどうなるでしょうか。図２の受注件数の分布、件数ゼロが5回、1件が3回、、、というデータはそのまま維持することにします。しかし、受注案件の発生はランダムですので、発生順序はランダムだとします。

これを実現するためには、表１の3列目の12個のデータからランダムに抜き取り、それを12回繰り返し並べた数値が次の1年間（2年目）の受注件数の推定値と考えます。2年目の受注件数の分布は、1年目のそれとは異なりますが、数値は、０、１、２、３、４で、それ以外はありません。100年分のデータを取るとどうなるか。図２とほぼ同じ形状の分布となるでしょう。但し、度数は100倍になります。

これって、何なの？　1年間の受注件数データから1,200回（12×100回）サンプリングしただけですので、サンプリング誤差も少なくなって、もともとのデータが再現された、だけの話じゃないの、ということですね。

なーんだ、といって、読むのをやめないでください。もう少し、お付き合いのほどを、、。

次に、量/件のデータを重ねていきます。受注件数ゼロでは受注数量もゼロです。計算する必要は有りません。受注件数1件ではどうなるか。このときの受注数量は図３の分布から、つまり7～13の15個のデータからランダムに1個の数値を抜き取ることになります。7～13以外の数値はありませんが、出現はランダムです。それを何回もやります。データ数15×100回で、1,500回としましょうか。で、受注数量の分布は？　受注件数の場合と同じで、受注件数1回の受注数量分布は、度数が100倍になるだけで、ほぼ図３と同じ。

またしても、なーんだ、といわれそうですね。

では、受注件数2件のときはどうなるか、考えてみます。表１の12月をみてください。受注件数は2件。量/件は7個と9個で、受注数量/月は16個。これは、7～13の15個の数値からランダムに2回抜き取り、それを加算したと考えます。これを繰り返します。1,500回にしましょう。2回抜き取り加算した数値を1,500個作る、でもいいですし、受注件数1件の1回抜取データ列に、もう1回抜き取ったデータを順に加えていってもいいと思います。

受注件数3件のときは、同様に3回抜き取った数値を合計した数値を1,500個作ります。つまり、受注件数と同じ回数だけ量/件のデータから抜き取って、合計した数値をあらかじめ決め抜取回数分、作ります。

図４に受注件数が1件～4件のときの受注数量の計算結果の棒グラフを示します。

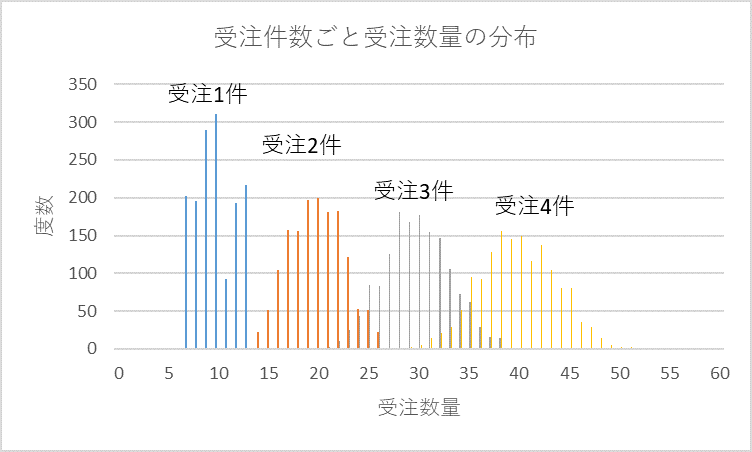
図4 受注件数ごとの受注数量の分布

受注1件の受注数量は図3のデータを抜き取っただけですので、抜取誤差を含んで多少ズレがありますが、図3の分布形状が保たれています。件数が2件、3件となるに従い分布形状は釣鐘状になってきます。

元々のデータ数は15個。受注件数1件のときはデータの組み合わせ数は15のまま。受注件数が2件では組み合わせ数が15×15=225。3件では15×15×15=3,375、4件では50,625となります。分布範囲は、1件では7～13ですが、2件では14～26、3件では21～39、4件では28～52となります。

計算は、これで終わりではありません。これまでの計算は、それぞれの受注件数の発生確率を１（100%）としてきましたが、実際は、図２に示すようにゼロ件は5回/12回（0.417）、1件は3回/12回（0.25）、2件は1回/12回（0.08）、3件は2回/12回（0.167）、4件は3回/12回（0.25）の発生確率です。受注数量の分布の確率が１となるようにそれぞれの発生確率をかけます。その結果、図5に、また、各件数の分布を合計した分布を図６に示します。

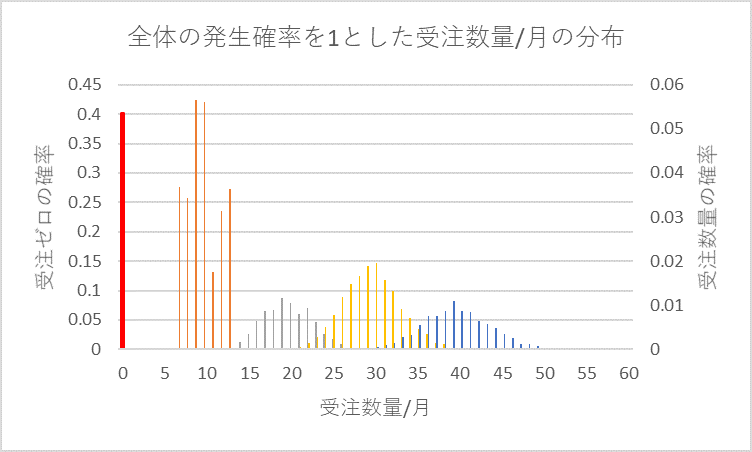
図5　発生確率を補正した受注数量/月の分布

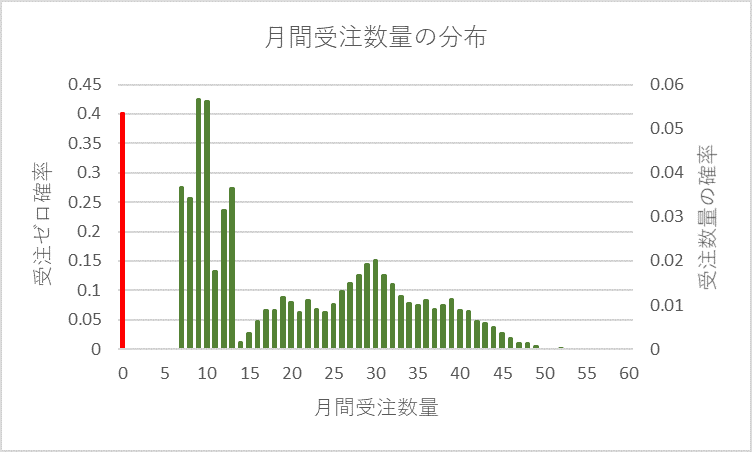
　図6 受注数量/月の全体の分布

累積確率カーブを図7に示します。

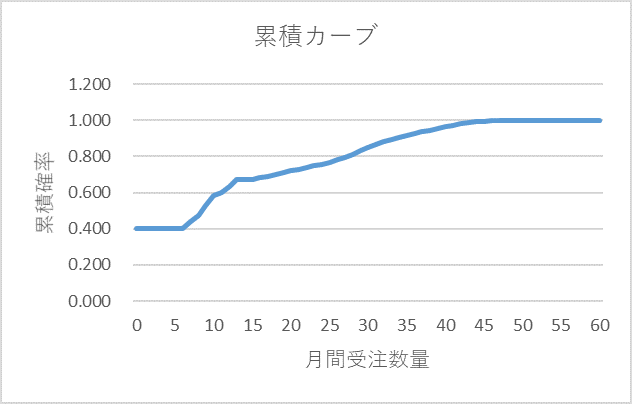
図7　受注数量の累積確率カーブ

累積確率カーブから、サービスレベルが80％、90％、95％、99％のときの月間需要数量を求めますと、図8のようになります。

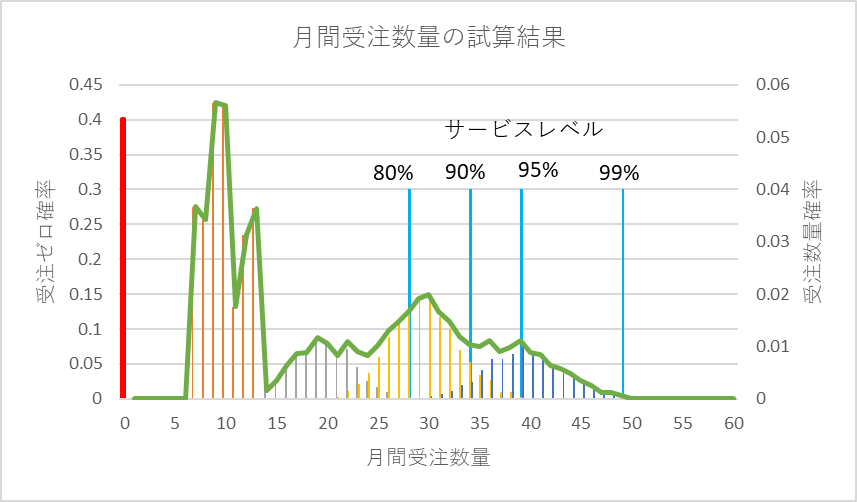
図8　受注数量の分布とサービスレベル

いかがでしょうか。手持ちのデータで作った図１が、需要の基本構造の仕組みを利用して推計すると図8のようになりました。サービスレベルも1％のステップで設定できるようになりました。確率分布のパラメータに頼ることなく、従ってどのような分布形状であろうと、需要のメカニズムを利用して、このような推定手法が可能であることをご承知おき頂ければ幸いです。

間欠需要は、一般的な需要からみれば、辺境的な環境条件です。受注数量はゼロ以下にはなりませんので、数量が少なくなる領域では、ゼロの壁に押し付けられるように変形します。しかし、これも物理現象として捉えると、いろいろと面白いことがわかってきます。次回もこのテーマで、ちょっと視点を変えて、愚見を述べてみたいと思います。

尚、ここでの計算はすべてエクセルを使っています。使った主な関数は、OFFSET（セルの位置指定）、RANDBETWEEN（範囲内のランダム値）、FREQUENCY（グラフの作成）です。ご質問のある方はこちらからお願いします。