No.78 リードタイムが変動すると、受注件数のバラツキはどうなる?
前回、納入リードタイムが変動する場合、その変動係数の二乗に受注件数平均の二乗をかけた分だけ、受注件数の分散が大きくなるという関係を見出しました。実に単純な関係ですが、現在の在庫管理論ではうまく導き出せないんです。その理由は、受注件数と1件当り受注数量(量/件)を識別していないから。識別しないと、在庫―受注―出荷―補充発注―入庫という在庫循環メカニズムを正しく捉えることができないんです。前回は数式モデルで説明しましたが、気になるのは分布形状。納入リードタイムの変動って、どのような分布形状で、それが受注件数のバラツキや分布にどのような影響があるのか、、。
例えば納入リードタイムが10日だとします。10日を中心に左右対称な分布になれば正規分布で近似できますが、直観的には、そうはならないような気がします。10日の納入リードタイムに対して、3日とか4日で納入されることは、、あまりないでしょうね。1日早く、あるいは2日早く納入される、なんていうのはあるかもしれませんが、、。総じて遅れることの方が多い。そうすると、分布形状は時間の進む方向にすそ野を引き、左右非対称になってしまいます。そんなことを考慮して、納入リードタイムを表すモデルを考えてみました。図1のように。
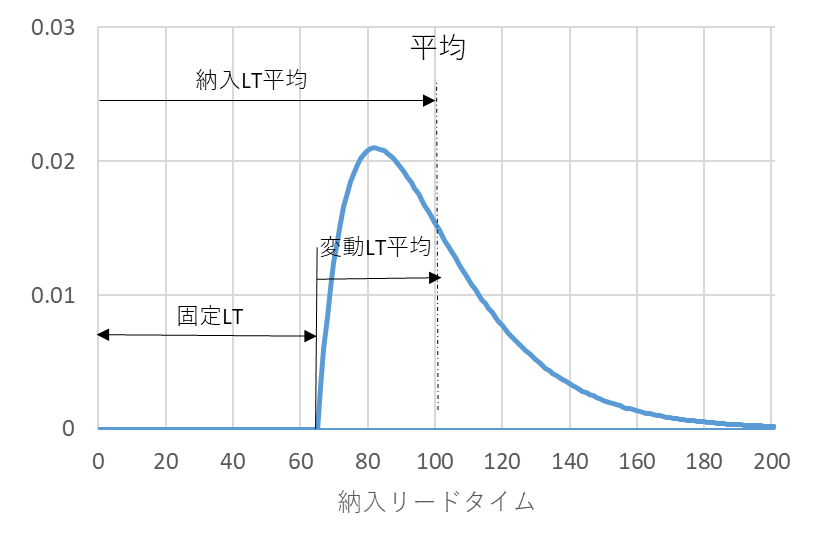
図1 納入リードタイムのモデルの一例
これ以上短くならない納入リードタイムを固定リードタイム、変動する部分をその平均と分布形状で表します。納入リードタイムの平均は固定リードタイムに変動リードタイム平均を加えたものになります。
で、分布形状はどのように表すか、ですが、その前に、なんで分布形状を気にしなければならないのか、確認しておきます。在庫管理の課題は、ザックリと言えば、在庫量最少・欠品率最小の妥協点を見つけること。多くの場合、その妥協点は、需要の分布が正規分布だとして求めるのが一般的です。
ところが、納入リードタイムのような時間分布は、前述のように、正規分布はあまり適さない。時間分布ではマイナス値はありませんが、正規分布はマイナスの値もある、という理由もあります。時間分布でよく使われるのが指数分布や指数分布に従う確率変数k個の和の分布であるアーラン分布です。
指数分布やアーラン分布は待ち行列理論ではお馴染みで、理論、応用例等充実していますので、納入リードタイムの分布として、アーラン分布(k=1のアーラン分布は指数分布)を使うのがいいかな、と思います。で、今回はさらに適用範囲を広げられないかという思いも込めて、指数分布やアーラン分布を包含するガンマ分布で試してみようか、と思います。(ガンマ分布の特別な条件で指数分布やアーラン分布になる)
待ち行列理論で分布形状をどのように捉えているのか、ザットみてみました。到着やサービスの分布は既知(あるいは仮定)として、待たされる確率、平均客数、待ち行列の平均長、平均待ち時間などを計算します。実用的にはこれでいいんでしょうが、今回は、待たされる時間、客数、行列の長さ、待ち時間の分布形状を知りたいんです。が、そのようのことに関する記述は。あるようでない。で、自分で、いろいろ、こねくり回して計算してみましたが、小生の数学の力では何ともならず、分布形状を求めることはできません。
暗中模索の中、思いついたのがシミュレーションソフト。在庫循環のメカニズムを視覚的に捉えて、様々な分布を利用して試行でき、シミュレーションデータもたくさんとることができますので、分布形状を比較的簡単に知ることができます。欠点は、ソフトがないとダメ、それとプログラミングが厄介。一般の方が利用するのは、ちょっと、抵抗が大きいでしょうか。
シミュレーションソフトがなくても、分布形状を確認する方法はないか。誰でも簡単に再現できる方法はないか。紆余曲折、辿りついたのはエクセル。エクセルを利用して、分布形状をみれるかもしれない、、と、、。
ガンマ分布関数はエクセルにもありますので、問題なく利用できます。では、エクセルでの計算例を紹介します。
納入リードタイムの分布形状の求め方を図2に示します。入力するデータは納入リードタイムの平均、その分散、固定リードタイムの3つ。残りの項目は次のようになります。
*![]()
* 納入LT変動係数=納入LT標準偏差/納入LT平均
* 変動LT平均=納入LT平均―納入固定LT
* 変動LT分散=納入LT分散
*![]()
* 変動LT変動係数=変動LT標準偏差/変動LT平均
*ガンマ分布;
*ガンマ分布;![]()
セルG3、G4には“=”の後に図で示した式を入れます(詳しくはエクセルの説明をご覧ください)。セルG5以降はG4をコピーすればOK。納入LT(リードタイム)分布表をグラフにすれば出来上がり。
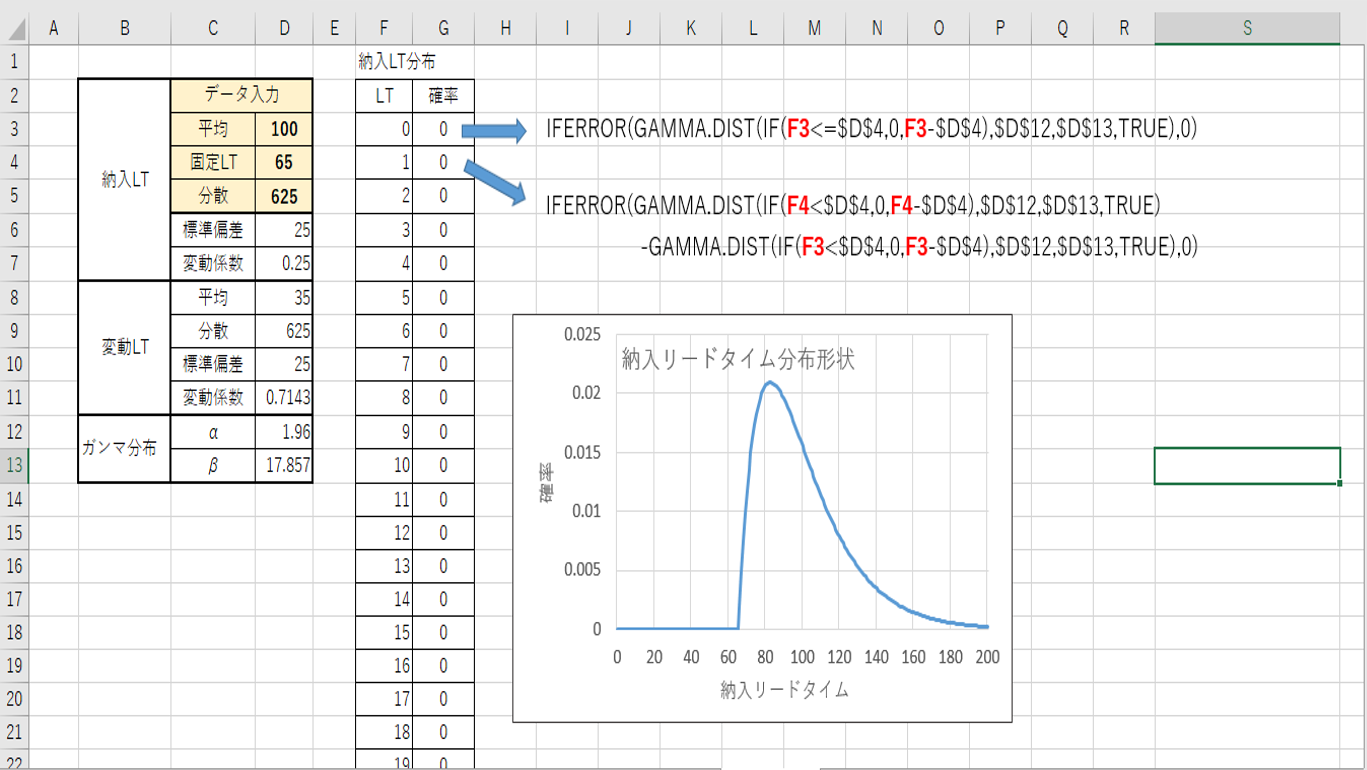
図2 納入リードタイムの分布形状の例
次に、受注件数の分布を作成します。ここでは納入リードタイムの変化分だけの影響を計算するため、受注間隔を一定にします。データは納入リードタイム間の受注件数平均を入力します。小数点の値でもかまいません。受注間隔平均=納入LT平均/受注件数平均 となり、受注間隔平均を一定値として計算します。セルM3、M4は図示の通り。M5以降はM4をコピー。受注件数分布表をグラフにします。
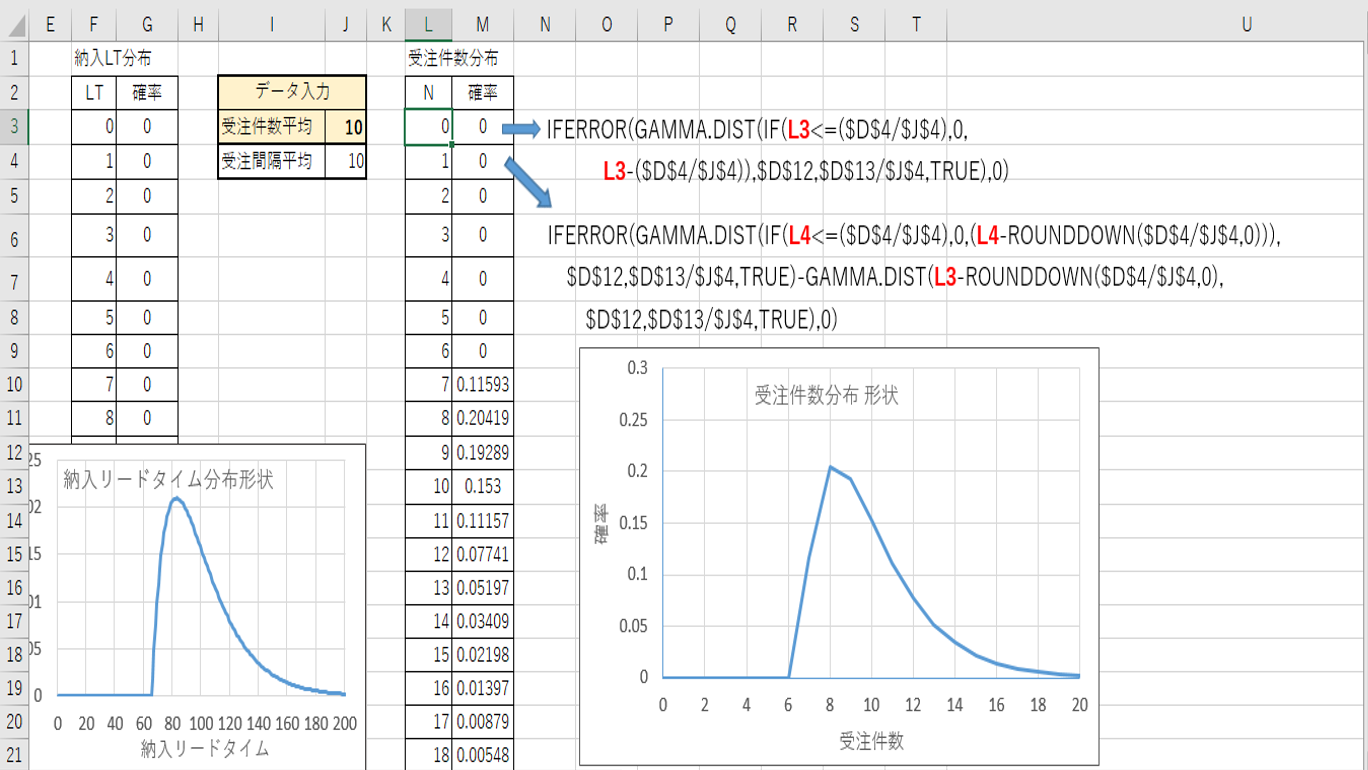
図3 受注件数の分布形状の一例
納入リードタイムの分布は時間軸に対して、その発生確率で捉えますが、受注件数は件数(ゼロ以上の整数)の発生確率で捉えます。つまり、単位が時間から件数に変換されます。
納入リードタイムの分布の時間軸は“1/受注間隔平均” で受注件数に変換されるだけですので、分布形状は同じようになります。但し、受注件数をカウントする時間単位でまとめられますので、その分ズレが生じます。
納入リードタイムの分布形状が異なる場合についてみてみます。表1にA、B、Cの3つの分布形状を示します。いずれも平均は100、変動係数は0.25です。計算した分布形状の一例を図4に示します。
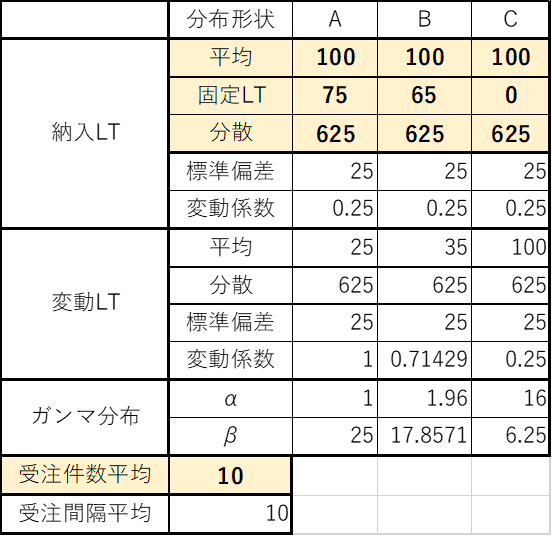
表1 納入リードタイム3種のデータ
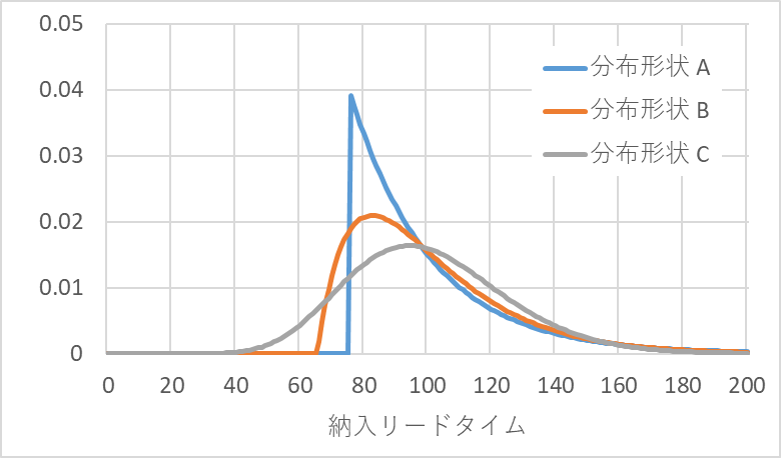
図4 3種の納入リードタイムの分布形状
図5はA、B、Cそれぞれの受注件数の分布形状です。A、B、Cいずれの分散も、
![]()
で同じになりますが、分布形状は異なります。
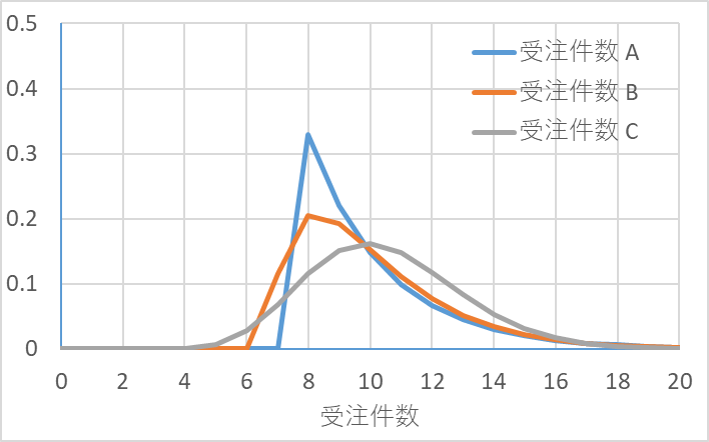
図5 3種の受注件数の分布形状
納入リードタイムと受注件数だけですが、エクセルで分布形状を捉えることができました。これを発展させると、受注量、出荷量、在庫量、、などの分布形状もエクセルで簡単に計算できるのではないでしょうか。